The following provides a set of steps for determining the size of the rocket on your camera sensor for the lens you are using, and your shooting location. These steps would apply for determining the size of any subject on your sensor, as long as you know the location of the subject and its physical size, your own location, your camera sensor format, and the lens focal length.
Rocket Size: The following link has the relevant technical data regarding the rocket size: cygnus-s-s-gene-cernan-to-resupply-station. The rocket is 139 feet tall, including the Cygnus payload fairing. There is no need to add the length of the Cygnus to the length of the rocket. Also note that It was planned to launch from Launch Pad 0-A.
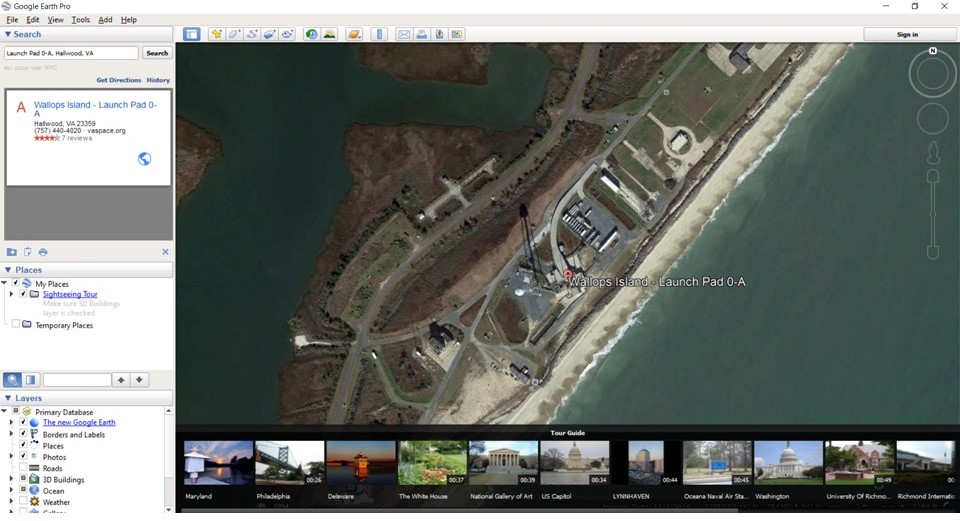
Distance to Pad: I used Google Earth to measure the distance from the photography site to the launch pad. You can download Google Earth Pro onto your computer for free, and try it out.
On the top/left of the screen, search on “Launch Pad 0-A”; it will show you “Launch Pad 0-A, Hallwood Va” as an option – pick this. It will rotate the earth and zoom in on the launch pad using a satellite map. It will mark the launch pad with an icon.
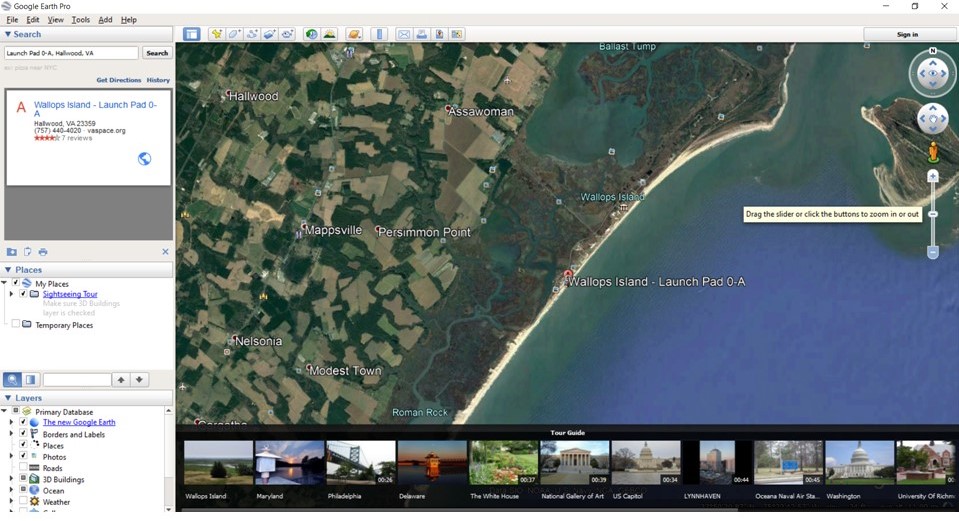
You can then use the zoom and scroll tools on the map screen to zoom out to include the photography site on the map. Since I promised not to say where the actual site is, you can just go to a spot on the other side of the wetlands from the launch pad, and pick a spot. You may have to then scroll around, and zoom in and hunt for your particular site, then zoom back out again, when you do this for a site of your own.
Measure distance by clicking on the ruler tool on the top tool bar. A pop up box will offer you some options. Select the measurement units in “feet”. Then move the mouse icon over your photography site location and click the mouse, drag the mouse over to the launch pad (trailing a yellow line along the way) and click again. The distance will show in the text box in feet. Make a note of it. In my case, it was 11,380 feet. Here is a made-up location example:
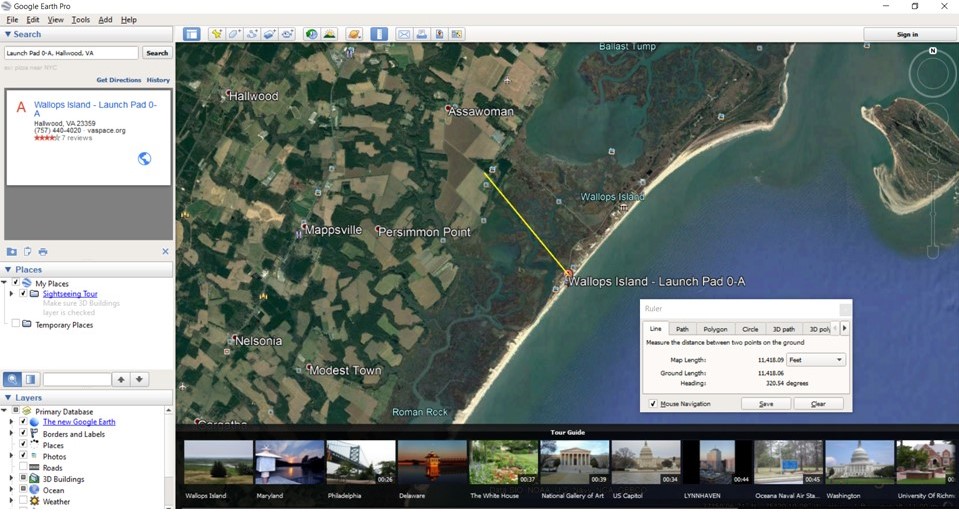
Click on Ruler tool on top tool bar, select ‘feet’, then click on shooting location and move to launch pad, and click again.
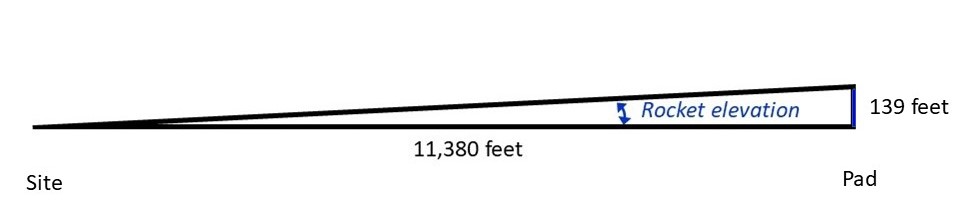
Rocket Angle: Now, knowing that the rocket is 139 feet tall, and the distance is 11,380 feet, I can determine what angular extent it represents from the site location.
If I divide the rocket height by the distance, the ratio gives me the rocket angular extent, but in a unit called “radians”, not in degrees. I will have to multiply by a conversion number to get degrees. For those that are alarmed that this isn’t how they learned to do trigonometry, this is an approximation to a trigonometry calculation that is simple and very accurate for small angles (of less than 10 degrees).
Rocket Elevation = 139’/11,380’ = 0.01221 radians
There are 57.3 degrees in one radian, so I multiply by this number to convert radians to degrees.
Rocket vertical angle = 0.01221 radians x 57.3 degrees per radian = 0.70 degrees.
OK, so now I know how tall the rocket will be as a vertical angle from me. Let’s look at the angle of view for some long telephoto lenses, and compare to the rocket angle.
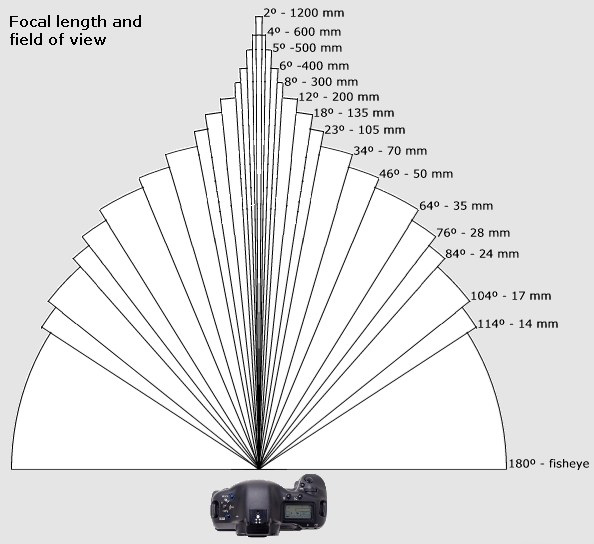
Angles of View for Lenses: The following site has a handy calculator for different camera sensor formats and lens focal lengths: depth-of-field-and-equivalent-lens-calculator
It lists a full frame camera as a “Nikon”. The brand is irrelevant. All full frame sensors are 36×24 mm. I put in my 560mm equivalent focal length lens (with my teleconverter), f/8, and 11,380 feet distance.
It shows me that I will have the following angles-of-view for my 560mm:
Horizontal 3.68°
Vertical 2.46°
If I didn’t own a teleconverter and only had 400mm, I would get larger angles-of-view:
Horizontal 5.15°
Vertical 3.44°
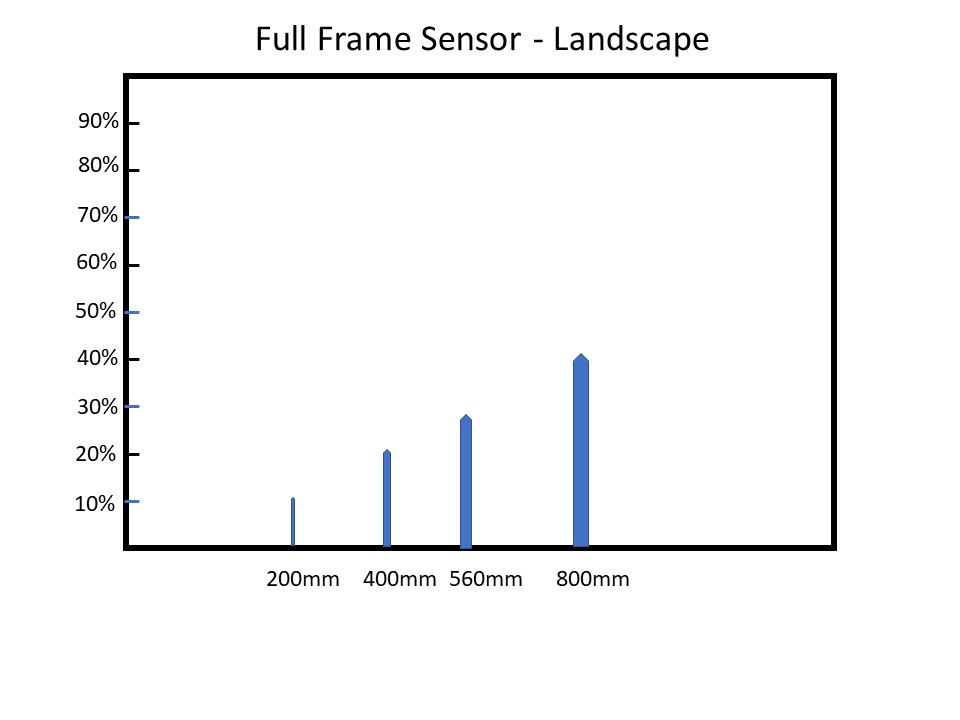
Rocket Size in Frame: The rocket is 0.70 degrees tall, and the vertical angle of coverage of my sensor with the 560mm focal length lens is 2.46 degrees. So, if I do a landscape mode (to capture the huge plume from ignition), the rocket will be the following fraction of the vertical size of my sensor: 0.70 degrees/2.46 degrees = 0.29 or 29%. This seems to be about perfect. I do want a border around the rocket. I don’t want to fill the viewfinder with the rocket, or I’ll lose it right after ignition. I want to take several shots as it leaves the launch pad, then adjust the zoom to back out.
If I used a 400mm lens, I would have 0.70/3.44 = 0.20 or 20%. At this point you can simply scale in your head to 200mm or 800mm lenses. A 200mm lens would result in the rocket being only 10% the size of your sensor (half of what you got for 400mm), while an 800mm lens would make it 40% (twice what you got for 400mm). By the way, the distance from the Visitors’ Center was about twice as far, so cut all of these sizes in half for that location.
If you’re like me you’re curious how this calculation compared to reality. The following image is an overlay of a photograph from the trip after I returned, and my prediction. I scaled a photograph of the launch pad and rocket (uncropped) to fit in my full frame sensor rectangle (in red) from the picture above, then moved the 560mm version of the modeled rocket (also from that picture above) up in the frame to sit alongside the real one. Hey, math works!